October 29, 2025
Headlines

tok exhibits

shm as a failure of acceleration

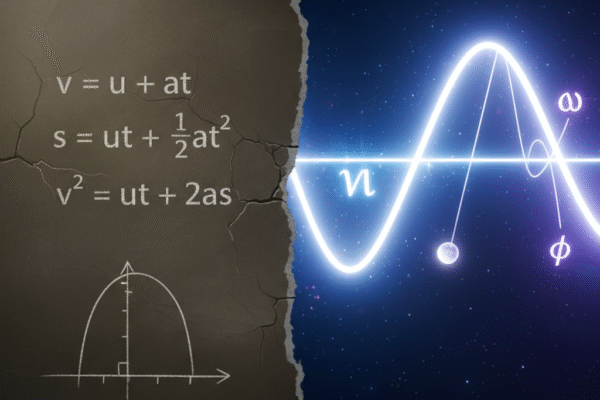
The Secret Language of Oscillations: Why Your Favorite Physics Equations Fail for SHM

rathankar010 mins

When Your Go-To Equations Give Up Think about the world around you: a pendulum swinging in a clock, a guitar string vibrating to make a note, or even a bungee jumper bouncing up and down. These are all examples of a special kind of rhythmic motion called Simple Harmonic Motion (SHM). In your physics class, you’ve probably become good friends with the kinematics equations: These equations are fantastic for figuring out the motion of a ball thrown in the air or a car accelerating down a road. But hereā€™s the puzzle: the moment you try to use them on a swinging pendulum or a bouncing spring, they completely fail. Why do these powerful tools fall silent when faced with the simple, repeating dance of SHM? Let’s find out. The Core Problem: A Constantly Changing Acceleration The kinematics equations you know and love have one critical weakness: they only work when acceleration is constant. For SHM, acceleration is the exact oppositeā€”it’s always changing! This leads to one of the most common misconceptions. Consider a typical exam question from one of our videos: The acceleration of the object is always proportional to its displacement, and it points in the opposite direction. Think of a spring: the more you stretch it (more displacement), the harder it pulls back (more acceleration). When the mass is at the center (zero displacement), the spring isn’t pulling at all, so the acceleration is zero. Because ‘a’ is never constant in SHM, you simply can’t plug it into v = u + at. We need a new set of tools. The Story of a Breakthrough: How We Cracked the Code Understanding SHM wasn’t a single “Eureka!” moment. It was a journey of discovery by some of history’s greatest scientific minds. Galileo’s Experiment: While sitting in a cathedral, Galileo noticed a lamp swinging [1]. Using his own pulse as a timer, he was amazed to find that each complete swing took the same amount of time, no matter how wide or narrow the swing was (for small angles). This told him there was a consistent rhythm, a constant period, to this motion. Hooke’s Law Hooke was obsessed with springs. He discovered a simple but powerful rule now called Hooke’s Law: the force a spring uses to pull back is directly proportional to how far you stretch it (F = -kx). This was the key! He found the mathematical reason for the changing acceleration. More stretch = more force = more acceleration. You can access his original paper at the internet archive [2] Isaac Newton (Late 1600s): Newton brought it all together. He took his Second Law of Motion (F=ma) and combined it with Hooke’s Law (F=āˆ’kx). This gave birth to the master equation of SHM: ma = -kx. This equation officially proved that acceleration (a) is not constantā€”it’s directly proportional to displacement (x). With his invention of calculus, Newton was able to solve this equation, giving us a whole new way to describe motion. The New Toolkit: Understanding Path and Phase Solving Newton’s master equation gives us a beautiful, wavy solution that looks like this: This might look complicated, but it introduces three powerful new concepts that perfectly describe SHM: This new language helps us solve problems that the old equations couldn’t touch. For example, understanding phase is key to answering questions like this: Video Example: A particle executes simple harmonic oscillations. What is the phase difference between the acceleration and the displacement of the particle? Let’s think about the very heart of Simple Harmonic Motion. An object in SHM is always being pulled back towards its center or equilibrium position. This “restoring force” is key. It means the direction of the force is always trying to counteract the object’s position. This leads to a classic question: In simple harmonic oscillations which two quantities always have opposite directions? Why Does This Matter? SHM is Everywhere! Understanding SHM isn’t just for passing exams; it’s fundamental to how the universe works. A Final Thought: Don’t Fear “Failed” Equations In TOK, we learn that scientific models are not reality itself; they are simplified maps designed for a specific purpose. The fact that your trusty kinematics equationsā€”a powerful model for constant accelerationā€”don’t work for SHM isn’t a failure. Instead, it’s a discovery of the model’s scope and limitations. šŸ—ŗļø This moment is an invitation to ask a classic knowledge question: To what extent does the failure of a scientific model contribute to the growth of knowledge? This situation perfectly demonstrates a core principle of the Natural Sciences as an Area of Knowledge (AOK): knowledge progresses not by proving things right, but by finding out where our current understanding is wrong. These “failures” are the catalysts for creating more comprehensive and powerful models. So, as a knower, embrace these moments. When a problem doesn’t fit your initial framework, it’s not a dead end. Itā€™s a sign that you are moving from a simple map to a more detailed one, pushing the boundaries of both your personal and shared knowledge. Keep questioning your assumptions, keep challenging your models, and keep exploring the rich complexity of the universe. šŸ¤” Bibliography:

Read More
sign convention problem in thermal physcis

The Sign Convention Headache in Thermal Physics: A Simple Fix for a Big Physics Problem

rathankar010 mins

Hello, physics students! Ever get a tricky heat problem wrong because of a simple plus or minus sign? Itā€™s one of the most common and frustrating mistakes. You did all the hard work, but a single sign tripped you up at the finish line. But what if I told you that for hundreds of years, the world’s best scientists had the exact same headache? This blog post tells the story of how they solved it, and how their simple solution is the key to you mastering these problems for good. The Problem: A Messy Past Long ago, scientists knew that heat moved from hot things to cold things. But they got stuck on a simple question: When heat moves, should we call it positive or negative? It was chaos. Some scientists would write “+50 Joules” to mean heat was gained. Others would use the exact same number to mean heat was lost. Imagine trying to build an engine if every engineer had their own definition of “up” and “down”! It was impossible to share research, repeat experiments, or even agree on the basics. The Solution: A Simple, Powerful Rule After years of confusion, scientists finally agreed on a rule that made everything clear. Itā€™s called the system-centric approach, which is a fancy way of saying: “Just focus on one thing at a time.” Hereā€™s the golden rule they created: That’s it! Think of it like a bank account. Money coming in is positive. Money going out is negative. The system is your account. Let’s See This Rule in Action! This single rule can help you solve problems from three different topics. Let’s break it down. 1. For Heating and Cooling Problems (Specific Heat) When you use a heater to warm up water, the water is your system. Heat is flowing INTO the water. Therefore, the heat energy (Q) is positive. If you let that hot water cool down, heat is flowing OUT, so Q would be negative. When you melt ice, you have to add heat to break the bonds and turn it into water. The ice is your system. Since heat is flowing INTO the ice, the heat required for melting (Q=mLā€‹) is positive. The same is true for boiling. Conversely, when steam condenses into water, it must release heat. The steam is the system, heat flows OUT, so the heat (Q=mLvā€‹) is negative. 3. For Mixing Problems (Calorimetry) This is where the sign convention becomes a lifesaver. Imagine you’re mixing hot metal into cold water. Since the heat lost by the metal is gained by the water, we get the most important equation in calorimetry: Q_gainedā€‹=āˆ’Q_lostā€‹ The minus sign is there to cancel out the negative sign from the heat that was lost, making sure the numbers balance perfectly. Why This “Small” Rule Changed the World Agreeing on this simple rule wasn’t just about making homework easier. It allowed engineers to design engines, chemists to understand chemical reactions, and scientists to model our planet’s climate. So the next time you see a plus or minus sign for heat, know that itā€™s not just a random ruleā€”itā€™s a powerful tool that brought order to chaos and helps us speak the universal language of science. Use it confidently. From Theory to Practice: Your Turn to Solve! Understanding the sign convention is the biggest step toward mastering calorimetry problems. But the best way to build lasting confidence is through practice. You need to see these principles in action again and again until they become second nature. Thatā€™s why Iā€™ve created a dedicated YouTube playlist that goes beyond just the sign convention. This playlist features worked examples from every major type of thermal physics problem, specifically designed to help you identify and eliminate all the common misconceptions. In the playlist, you will find detailed solutions for problems covering: By working through these problems, you’ll build the skills and confidence to solve any thermal physics question that comes your way. Ready to get started? [Click Here to Access the Full Thermal Physics Misconceptions Playlist on YouTube]

Read More
resistance and resistivity misconceptions

That Annoying Wire Problem: 3 Physics Traps You Keep Falling For

rathankar07 mins

You know the one Iā€™m talking about. The question about two copper wiresā€”one thick, one thinā€”and you have to figure out the resistance. You use the formula, you double-check your math, but your answer is still wrong. Sound familiar? It’s one of the most common frustrations in electricity, but I promise, it’s not as hard as it looks. You’re likely falling for one of three sneaky traps that catch almost everyone. Let’s expose them, fix them, and make sure you nail these questions every single time. Trap #1: The Identity Crisis ā€” Mixing Up Resistance and Resistivity Okay, let’s be honest. “Resistance” and “Resistivity” sound almost the same. Itā€™s easy to think they are. This is the #1 reason students get confused. Here’s the only analogy you’ll ever need: Resistivity is like a material’s DNA. Resistance is how that material behaves in the real world. Every piece of copper in the universe has the same resistivity (Ļ). It’s a fundamental property, like its color or density. You can’t change it unless you change the material itself. You an view a video that clearly explains how resistivity remains same for wires of different lengths and thickness here But a wire’s resistance (R) depends on its shape. A long, skinny copper wire will put up a huge fight against current (high resistance), while a short, fat copper wire will let it flow easily (low resistance). So, when a question says “two wires are made of the same material,” your brain should immediately think: “Aha! Same resistivity.” Simple change, but it makes all the difference. Trap #2: The Sneakiest Trick in the Book ā€” The Diameter Trap This one feels like it was designed to trick you. The question says, “The diameter of a wire is doubled,” and your gut reaction is, “Great! Resistance is cut in half.” WRONG. Remember, the electricity doesn’t care about the diameter. It cares about the total space it has to move through, which is the cross-sectional area. Letā€™s look at the formula: R=ĻALā€‹ Itā€™s all about the Area (A). And whatā€™s the formula for the area of a circle? A=Ļ€r2. See that little ‘squared’ symbol? Thatā€™s the trap. Let’s walk through it: So, if you double a wire’s thickness, you make the path for the current four times larger. This means the resistance drops to one-quarter of its original value. If you want to see this in action, check out our video where we solve this exact type of problem step-by-step! Trap #3: The “Wait, What?” Unit Confusion We all know resistance is measured in Ohms (Ī©). But on a multiple-choice test, you might see options like VAāˆ’1 or WAāˆ’2 and have a mini-panic. Don’t sweat it. A unit for a physical quantity can come from any valid equation it’s in. It’s a perfectly correct, just less common, unit for resistance. Seeing this shows you understand the concepts, not just one formula. Your New Cheat Sheet for Wire Problems Tired of falling for these traps? Here are your new rules: That’s it. These three ideas are the key. Master them, and that annoying wire problem will become one of the easiest questions on your test. You’ve got this. For clarifying more such misconceptions to solve resistance and resistivity problems without committing any mistakes, view all the problems from this playlist.

Read More